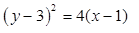ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
Encontre a medida dos semieixos, os focos e a excentricidade da elipse 16 x 2 + 36 y 2 = 576.
a = 6, b = -4, F1(-2√5,0) e F2(-2√5,0), e = √5
a = 6, b = 4, F1(-2√5,0) e F2(2√5,0), e = √5/3
a = -4, b = 6, F1(√5,0) e F2(-√5,0), e = √5/3
a = 4, b = 6, F1(-√5,0) e F2(√5,0), e = √5
a = -6, b = 4, F1(2√5,0) e F2(-2√5,0), e = √5/3
Determine os focos e a excentricidade da elipse 9 x 2 + 5 y 2 – 45 = 0.
F1(-5,0) e F2(3,0), e = 2/5
F1(0,-2) e F2(0,2), e = 2/3
F1(-3,0) e F2(5,0), e = √5/2
F1(2,0) e F2(0,-2), e = 2/√5
F1(-2,0) e F2(2,0), e = 2/√5
O planejamento de um bairro de uma cidade com grande expansão populacional foi feito considerando uma região plana, com quadras de mesma dimensão sendo delimitadas por ruas paralelas e perpendiculares. O esboço desse projeto foi realizado e feita uma representação do bairro no plano cartesiano localizando-o no segundo quadrante, no qual as distâncias nos eixos coordenados são consideradas em quilômetros, conforme figura exposta a seguir.
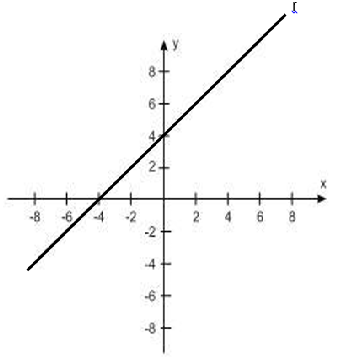
O percurso de uma linha de transporte coletivo que atravessará o bairro e outras regiões da cidade é representado pela reta r. Considere que no ponto P1 de coordenadas ( - 5 , 5 ) localiza-se um hospital universitário público e no ponto P2 , de coordenadas ( x , y ), um ponto de transporte coletivo. Assinale a alternativa que expressa a localização de P2 de forma que sua distância em relação ao hospital, medida em linha reta, não seja maior que 5 km e a equação que representa a reta r.
P2 ( - 3 , 1 ), r : y = - x + 4.
P2 ( - 3 , 1 ), r : y = x + 4.
P2 ( 2 , 6 ), r : y = x + 4.
P2 ( 0 , 4 ), r : y = x - 4.
P2 ( - 5 , 0 ), r : y = x + 4.

a = 6, b = -4, F1(-2√5,0) e F2(-2√5,0), e = √5
a = 6, b = 4, F1(-2√5,0) e F2(2√5,0), e = √5/3
a = -4, b = 6, F1(√5,0) e F2(-√5,0), e = √5/3
a = 4, b = 6, F1(-√5,0) e F2(√5,0), e = √5
a = -6, b = 4, F1(2√5,0) e F2(-2√5,0), e = √5/3
Determine os focos e a excentricidade da elipse 9 x 2 + 5 y 2 – 45 = 0.
F1(-5,0) e F2(3,0), e = 2/5
F1(0,-2) e F2(0,2), e = 2/3
F1(-3,0) e F2(5,0), e = √5/2
F1(2,0) e F2(0,-2), e = 2/√5
F1(-2,0) e F2(2,0), e = 2/√5
O planejamento de um bairro de uma cidade com grande expansão populacional foi feito considerando uma região plana, com quadras de mesma dimensão sendo delimitadas por ruas paralelas e perpendiculares. O esboço desse projeto foi realizado e feita uma representação do bairro no plano cartesiano localizando-o no segundo quadrante, no qual as distâncias nos eixos coordenados são consideradas em quilômetros, conforme figura exposta a seguir.

O percurso de uma linha de transporte coletivo que atravessará o bairro e outras regiões da cidade é representado pela reta r. Considere que no ponto P1 de coordenadas ( - 5 , 5 ) localiza-se um hospital universitário público e no ponto P2 , de coordenadas ( x , y ), um ponto de transporte coletivo. Assinale a alternativa que expressa a localização de P2 de forma que sua distância em relação ao hospital, medida em linha reta, não seja maior que 5 km e a equação que representa a reta r.
P2 ( - 3 , 1 ), r : y = - x + 4.
P2 ( - 3 , 1 ), r : y = x + 4.
P2 ( 2 , 6 ), r : y = x + 4.
P2 ( 0 , 4 ), r : y = x - 4.
P2 ( - 5 , 0 ), r : y = x + 4.

F1(-5,0) e F2(3,0), e = 2/5
F1(0,-2) e F2(0,2), e = 2/3
F1(-3,0) e F2(5,0), e = √5/2
F1(2,0) e F2(0,-2), e = 2/√5
F1(-2,0) e F2(2,0), e = 2/√5
O planejamento de um bairro de uma cidade com grande expansão populacional foi feito considerando uma região plana, com quadras de mesma dimensão sendo delimitadas por ruas paralelas e perpendiculares. O esboço desse projeto foi realizado e feita uma representação do bairro no plano cartesiano localizando-o no segundo quadrante, no qual as distâncias nos eixos coordenados são consideradas em quilômetros, conforme figura exposta a seguir.

O percurso de uma linha de transporte coletivo que atravessará o bairro e outras regiões da cidade é representado pela reta r. Considere que no ponto P1 de coordenadas ( - 5 , 5 ) localiza-se um hospital universitário público e no ponto P2 , de coordenadas ( x , y ), um ponto de transporte coletivo. Assinale a alternativa que expressa a localização de P2 de forma que sua distância em relação ao hospital, medida em linha reta, não seja maior que 5 km e a equação que representa a reta r.
P2 ( - 3 , 1 ), r : y = - x + 4.
P2 ( - 3 , 1 ), r : y = x + 4.
P2 ( 2 , 6 ), r : y = x + 4.
P2 ( 0 , 4 ), r : y = x - 4.
P2 ( - 5 , 0 ), r : y = x + 4.


P2 ( - 3 , 1 ), r : y = - x + 4.
P2 ( - 3 , 1 ), r : y = x + 4.
P2 ( 2 , 6 ), r : y = x + 4.
P2 ( 0 , 4 ), r : y = x - 4.
P2 ( - 5 , 0 ), r : y = x + 4.